Circumcenter Calculator

Circumcenter Calculator

Circumcenter calculator helps to calculate the circumcenter of a triangle.

How circumcenter of a triangle calculator works?

The triangle circumcenter calculator calculates the circumcenter of triangle with steps. Follow these steps to find the circumcenter using the circumcenter finder.

• Enter the coordinates for points A, B, and
• Click the Calculate button to see the result.
• Use Reset button to enter new values.

Circumcentre of a triangle calculator will instantly show you the circumcenter for the given coordinates.

What is circumcenter?

Circumcenter of a triangle is the point of intersection of all three perpendicular bisectors of the triangle. Perpendicular bisectors are nothing but the line or a ray that cuts another line segment into two equal parts at 90 degrees.
The circumcenter's position depends on the type of triangle:

• the circumcenter lies inside the triangle (acute angle)
• the circumcenter lies outside the triangle (obtuse angle)
• the circumcenter lies at the center of the hypotenuse (right angle)

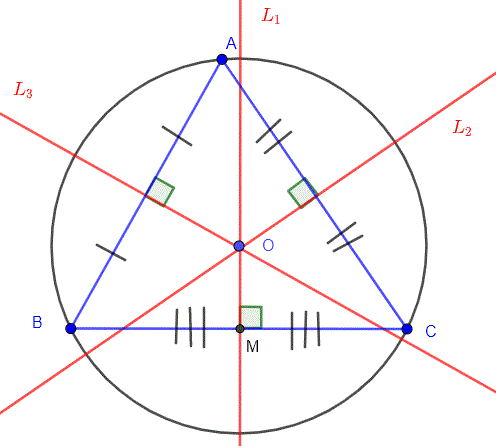
How to find the circumcenter of a triangle?

Wondering how to calculate circumcenter without using circumcenter formula calculator? Well, there is no specific circumcenter formula to find it.

The circumcenter of a triangle can be found as the intersection of any two of the three perpendicular bisectors. The method to find circumcenter of triangle is given below.

• Find the midpoint of each side of the triangle.
• Find the slope of line.
• Calculate equation of line using slope and midpoint.

y-y₁ = m (x-x₁)

• Get the equation of all remaining lines using their midpoints and slope.
• Calculate intersection point by evaluating two bisector equations.
• The intersection point obtained in previous step is the circumcenter of triangle.

Example:

Find the circumcenter of triangle whose vertices are (5, 4), (3, 1), (6, 1).

Solution:

Step 1: First of all, we will calculate the midpoint for each line of triangle. We will have lines AB, and BC.

Let,

A = (5, 4)

B = (3, 1)

C = (6, 1)

Suppose, D = midpoint of AB and E = midpoint of BC.

Midpoint of AB

D = [(x₁ + x₂)/2, (y₁ + y₂)/2]

D = [(5 + 3)/2, (4 + 1)/2]

Midpoint of AB = D = (4, 5/2)

Midpoint of BC

E = [(x₁ + x₂)/2, (y₁ + y₂)/2]

E = [(3 + 6)/2, (1 + 1)/2]

Midpoint of BC = E = (9/2, 1)

Step 2: Now, we will calculate the slope of line.

Slope of AB

Slope of AB = [(y₂ - y₁)/(x₂ - x₁)] = [(1 - 4)/(3 - 5)]

Slope of AB = 3/2

Slope of the perpendicular line to AB = -1/ Slope of AB = -1/(3/2) = -2/3

Slope of BC

Slope of BC = [(y₂ - y₁)/(x₂ - x₁)] = [(1 - 1)/(6 - 3)]

Slope of BC = 0

Slope of the perpendicular line to BC = -1/ Slope of BC = -1/0 = 0

Step 3: Find the equation of line.

Equation of the line AB

y = mx + b

Where m refers to the slope of perpendicular line. Place the value of slope of perpendicular line AB, m = -2/3 in above equation.

y = -2/3(x) + b ------------>(1)

Place the midpoint vertices of line AB, D = (4, 5/2) in equation 1.

5/2 = -2/3(4) + b

b = 5.17

Substitute b in equation 1.

y = -2/3(x) + 5.17 -------------->(2)

Equation of the line BC

y = mx + b

Substitute the value of slope of perpendicular line BC, m = 0 in above equation.

y = 0x + b

y = b ------------>(3)

Place the midpoint vertices of line BC, E = (9/2, 1) in equation 3.

b = 1

Substitute b in equation 3.

y = 1 -------------->(4)

Step 4: We have got the value of y. Now we have to find the value of x by substituting equation 4 in equation 2.

1 = -2/3(x) + 5.17

x = -3/2(1 – 5.17)

x = -3/2(-4.17)

x = 6.25

So, x = 6.25 and y = 1

Circumcenter of triangle ∆ABC = (6.25, 1)

Don’t want to waste time doing all of the above stuff? Use the circumcenter solver above to save your precious time.