Calculadora de integral

Calculadora Integral é uma ferramenta on-line que calcula a antideriva de uma função. Ele funciona como uma calculadora integral definida, bem como uma calculadora integral indefinida e permite resolver o valor integral em nenhum momento.

Calculadora de integração de linha mostra todas as etapas necessárias para avaliar as integrais. Ele realiza a integração de uma função por partes e resolve as integrais com dois métodos diferentes.

O que é uma integral?

Uma integral é o reverso do derivado. Pode ser usado para determinar a área sob a curva.

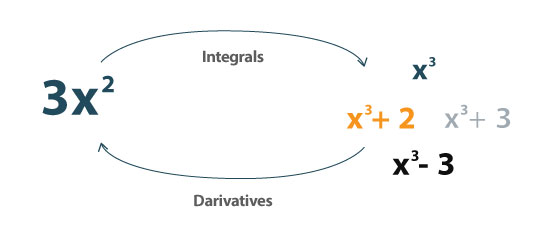
Pode ser definido como:

"Uma integral atribui números a funções de uma maneira que possa descrever o deslocamento, área, volume e outros conceitos que surgem combinando dados infinitesimais. A integração é uma das duas principais operações de cálculo; Sua operação inversa é diferenciação (tomando derivativos) ".

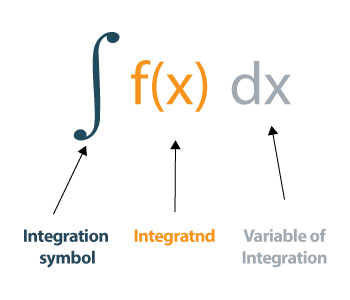
Como avaliar as integrais?

Você pode saber como resolver integrs manualmente. Pode ser de alguma forma irritante para aqueles que estão apenas começando com integrais. Mas não se preocupe. Vamos demonstrar os cálculos com exemplos para que você possa segurá-lo facilmente.

Vamos usar um exemplo para entender o método para calcular a integral definida.

Exemplo - Integral definido

Para a função f (x) = x - 1, encontre a integral definida se o intervalo for [1, 10].

Solução:

Etapa 1: determine e anote a função f (x).

F (x) = x – 1

Interval = [1, 10]

Etapa 2: Tome a antiderinativa da função e adicione a constante.

= ∫ (x−1) dx = (x²/2) – x + C

Etapa 3: Calcular os valores do limite superior F (A) e limite inferior F (B).

Como, a = 1 e b = 10,

F(a) = F(1) = (1²/2) - 1 = -0.5

F(b) = F(10) = (10²/2) - 10 = 40

Passo 4: Calcule a diferença de limite superior F (a) e limite inferior F (B).

F (b) – F (a) = 40 – (-0.5) = 40.5

Você pode usar uma calculadora integral dupla acima para se você não quiser entrar em cálculos integrais.

Exemplo - Integral de uma função trigonométrica

Para a função f (x) = pecado (x), encontre a integral definida se o intervalo for [0, 2π].

Solução:

Etapa 1: anote a função.

F (x) = sin (x)

Interval = [0, 2π]

Etapa 2: Tome a antiderivação da função e adicione constante C.

= ∫ sin(x)dx = - cos(x) + C

Etapa 3: Calcular os valores do limite superior F (A) e limite inferior F (B).

Como, a = 0 e b = 2π,

F (a) = F (0) = cos (0) = 0

F (b) = F (2π) = cos (2π) = 0

Passo 4: Calcule a diferença de limite superior F (a) e limite inferior F (B).

F (b) – F (a) = 0 – 0 = 0

Use solucionador integral acima para resolver uma integral trigonométrica em uma fração de segundos.