To calculate result you have to disable your ad blocker first.
Integrály kalkulačka
Zadejte funkci, proměnnou, horní a dolní mez vázaného. Vyberte možnost definitivní nebo neurčitou. Stiskněte tlačítko Vypočítat, abyste zhodnotili integrální krok za krokem pomocí antiderivativní kalkulačky.
Table of Contents:
Integrální kalkulačka je online nástroj, který vypočítává antiderivaci funkce. Pracuje jako definitivní integrální kalkulačka, stejně jako neurčitou integrální kalkulačku a umožňuje vyřešit integrální hodnotu v žádném okamžiku.
Line Integration Calculator zobrazuje všechny kroky potřebné k vyhodnocení integrálů. Provádí integraci funkce podle dílů a řeší integrály se dvěma různými metodami.
Co je integrál?
Integrál je opačný od derivátu. Lze jej použít k určení oblasti pod křivkou.
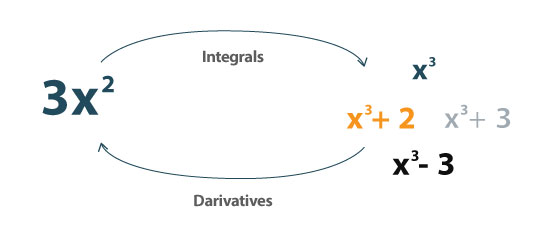
Lze definovat jako:
"Integrální přiřazuje čísla pro funkce, které mohou popsat posunutí, oblast, objem a další pojmy, které vznikají kombinací infinitézálních dat. Integrace je jednou ze dvou hlavních operací pro počet; Jeho inverzní operace je diferenciace (užívání derivátů). "
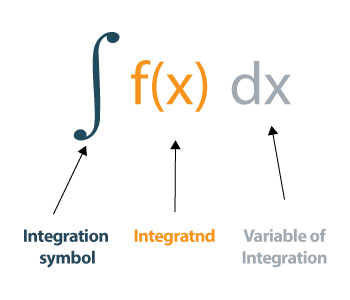
Jak hodnotit integrály?
Možná budete chtít vědět, jak ručně vyřešit integrály. To může být nějakým způsobem nepříjemné pro ty, kteří právě začínají integrály. Ale nebojte se. Výpočty s příklady demonstrujeme, abyste ji snadno pochopili.
Použijte příklad k pochopení metody pro výpočet definitivního integrálu.
Příklad - definitivní integrál
Pro funkci f (x) = x - 1 najít definitivní integrál, pokud je interval [1, 10].
Řešení:
Krok 1: Určete a zapište funkci F (x).
F (x) = x – 1
Interval = [1, 10]
Krok 2: Vezměte antiderivaci funkce a přidejte konstantu.
= ∫ (x−1) dx = (x2/2) – x + C
Krok 3: Vypočítejte hodnoty horního limitu F (a) a dolního limitu f (b).
As, a = 1 a b = 10,
F(a) = F(1) = (12/2) - 1 = -0.5
F(b) = F(10) = (102/2) - 10 = 40
Krok 4: Vypočítejte rozdíl v horním limitu F (a) a dolním limitu f (b).
F (b) – F (a) = 40 – (-0.5) = 40.5
Můžete použít dvojitou integrální kalkulačku výše, pokud nechcete dopřát integrální výpočty.
Příklad - integrál trigonometrické funkce
Pro funkci f (x) = hřích (x), najít určitý integrál, pokud je interval [0, 2π].
Řešení:
Krok 1: Zapište si funkci.
F (x) = sin (x)
Interval = [0, 2π]
Krok 2: Vezměte antiderivaci funkce a přidejte konstantu C.
= ∫ sin(x)dx = - cos(x) + C
Krok 3: Vypočítejte hodnoty horního limitu F (a) a dolního limitu f (b).
As, a = 0 a b = 2π,
F (a) = F (0) = cos (0) = 0
F (b) = F (2π) = cos (2π) = 0
Krok 4: Vypočítejte rozdíl v horním limitu F (a) a dolním limitu f (b).
F (b) – F (a) = 0 – 0 = 0
Použijte integrální řešitel výše, abyste vyřešili trigonometrický integrál ve zlomku sekund.