To calculate result you have to disable your ad blocker first.
Standardabweichung Rechner
Geben Sie die Stichproben- oder Grundgesamtheitswerte durch Kommas getrennt ein, um die Standardabweichung mit diesem Rechner zu ermitteln.
Table of Contents:
Standardabweichungsrechner
Der SD-Rechner wird zur Berechnung der Standardabweichung und der anderen zur Berechnung der Standardabweichung erforderlichen Werte verwendet. Zu diesen Werten gehören:
- Varianz
- Zählen
- Anzahl von Beispielen
- Quadratsumme
Mit diesem Standardabweichungsrechner können Sie die Standardabweichung sowohl für die Stichprobe als auch für die Grundgesamtheit ermitteln.
Was ist die Standardabweichung?
„Die Standardabweichung ist ein Maß für das Ausmaß der Variation oder Streuung einer Reihe von Werten.
Wenn die Werte in einem Datensatz nahe beieinander liegen, z. B. 2,3,4, ist der Wert der Standardabweichung klein. Wenn die Werte hingegen größere Unterschiede aufweisen, z. B. 1,18,90, dann ist der Wert der Standardabweichung hoch.
Standardabweichungsformel:
Die Formel der Standardabweichung ist weitgehend dieselbe wie die der Varianz.
Für Bevölkerung:
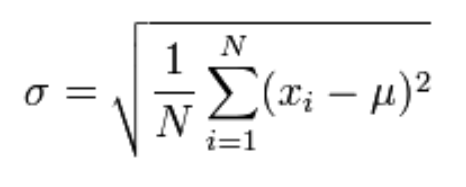
Zum Beispiel:
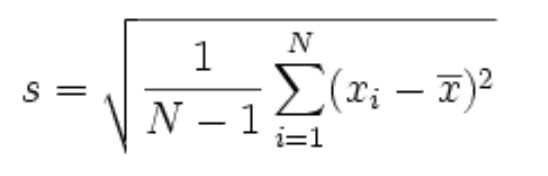
Wo
- σ,s = Standardabweichung
- µ, x̅ = Mittelwert
- X ich = Einzelne Werte
- N = Zählen
Formel für den Bevölkerungsmittelwert:
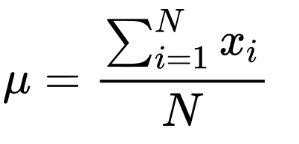
Beispielformel für den Mittelwert:
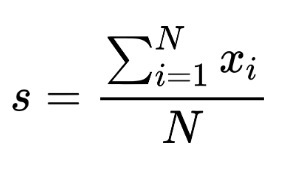
Wie finde ich die Standardabweichung?
Die Berechnung der Standardabweichung umfasst viele Schritte und wird ermüdend, wenn der Datensatz eine große Anzahl von Werten enthält. Die beste Option ist die Verwendung des oben genannten Standardabweichungsrechners.
Aber für diejenigen, die den manuellen Prozess erlernen möchten, finden Sie unten ein Beispiel, das alle Berechnungen erklärt.
Beispiel:
Ermitteln Sie für den folgenden Datensatz die Standardabweichung.
1,3,5,7,9,11,13,15
Lösung:
Schritt 1: Zählen Sie die Werte.
N = 8
Schritt 2: Ermitteln Sie den Mittelwert der Stichprobe.
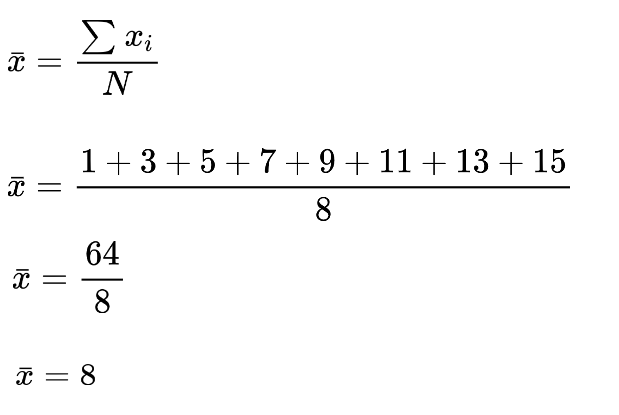
Schritt 3: Ermitteln Sie das Quadrat der Differenz der Werte vom Mittelwert.
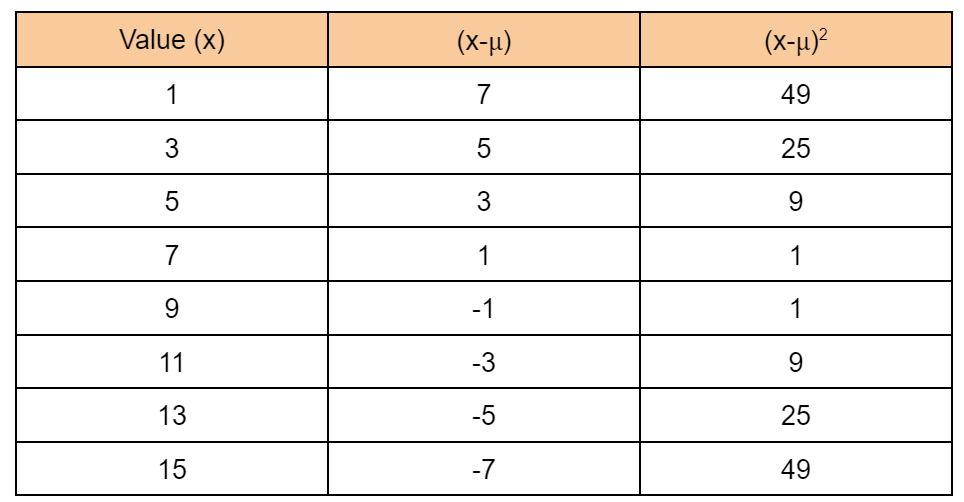
Schritt 4: Finden Sie die Summe von (x-µ) 2 .
= Σ(x-µ) 2
= 49+25+9+1+1+9+25+49
= 168
Schritt 5: Varianz berechnen.
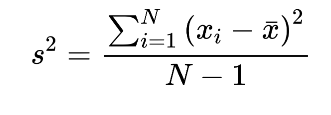
= 168/8-1
= 168/7
= 24
Schritt 6: Ziehen Sie die Quadratwurzel der Varianz, um die Standardabweichung zu ermitteln.
s = (24) 1/2
S = 4,89