To calculate result you have to disable your ad blocker first.
Calculadora De Desviacion Estandar
Ingrese los valores de muestra o población, separados por comas, para encontrar la desviación estándar usando esta calculadora.
Table of Contents:
Calculadora de desviación estándar
La calculadora SD se utiliza para calcular la desviación estándar y los otros valores necesarios para calcular la desviación estándar. Estos valores incluyen:
- Variación
- Contar
- Número de muestras
- Suma de cuadrados
Puede utilizar esta calculadora de desviación estándar para encontrar la desviación estándar tanto para la muestra como para la población.
¿Cuál es la desviación estándar?
"El Desviación Estándar "Es una medida de la cantidad de variación o dispersión de un conjunto de valores".
Si los valores de un conjunto de datos están cerca uno del otro, por ejemplo 2,3,4, entonces el valor de la desviación estándar es pequeño. Por el contrario, cuando los valores tienen mayores diferencias, por ejemplo 1,18,90, entonces el valor de la desviación estándar es alto.
Fórmula de desviación estándar:
La fórmula de la desviación estándar es muy parecida a la de la varianza.
Para población:
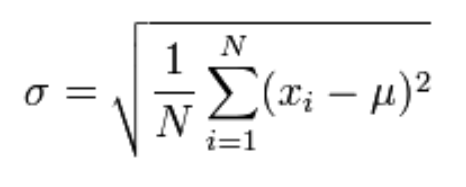
Para muestra:
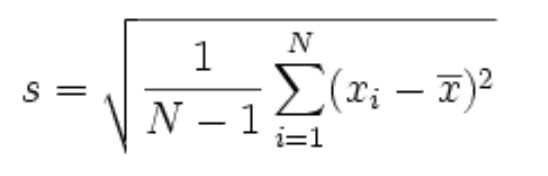
¿Dónde?
- ,s = Desviación estándar
- µ, x̅ = Media
- X i = Valores individuales
- norte = Contar
Fórmula de media poblacional:
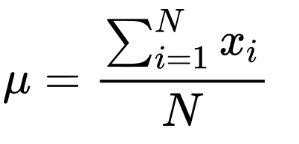
Fórmula media de muestra:
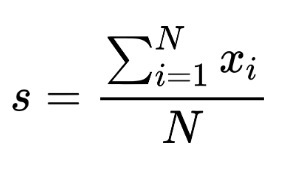
¿Cómo encontrar la desviación estándar?
El cálculo de la desviación estándar comprende muchos pasos y resultará agotador cuando el conjunto de datos contenga una gran cantidad de valores. La mejor opción es utilizar la calculadora de desviación estándar anterior.
Pero para aquellos que quieran aprender el proceso manual, a continuación se muestra un ejemplo que explicará todos los cálculos.
Ejemplo:
Para el siguiente conjunto de datos, encuentre la desviación estándar.
1,3,5,7,9,11,13,15
Solución:
Paso 1: Cuente los valores.
norte = 8
Paso 2: Encuentre la media de la muestra.
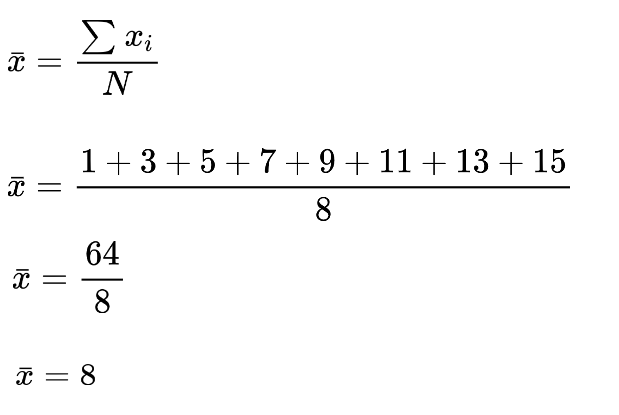
Paso 3: Encuentra el cuadrado de la diferencia de valores con respecto a la media.
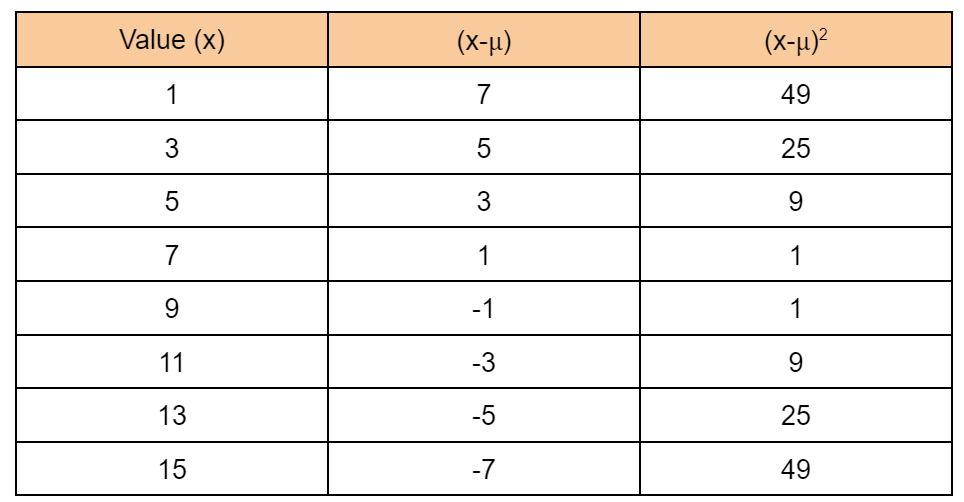
Etapa 4: Encuentra el suma de (x-µ) 2 .
= Σ(x-µ) 2
= 49+25+9+1+1+9+25+49
= 168
Paso 5: Calcular la varianza.
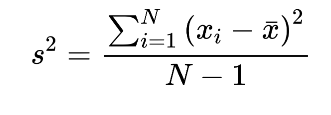
= 168/8-1
= 168/7
= 24
Paso 6: Saca la raíz cuadrada de la varianza para encontrar la desviación estándar.
s = (24) 1/2
s = 4,89