To calculate result you have to disable your ad blocker first.
Calcolatrice integrale
Inserire la funzione, la variabile, il limite superiore e inferiore del limite. Seleziona l'opzione definita o indefinita. Premi il pulsante calcola per valutare il passo integrale tramite passo utilizzando il calcolatore antiderivativo.
Table of Contents:
Integral Calculator è uno strumento online che calcola l'antiderivativo di una funzione. Funziona come una calcolatrice integrale definita e un calcolatore integrale indefinito e consente di risolvere il valore integrale in pochissimo tempo.
La calcolatrice di integrazione della linea mostra tutti i passaggi necessari per valutare gli integrali. Esegue l'integrazione di una funzione per parti e risolve gli integrali con due metodi diversi.
Qual è un integrale?
Un integrale è il contrario del derivato. Può essere utilizzato per determinare l'area sotto la curva.
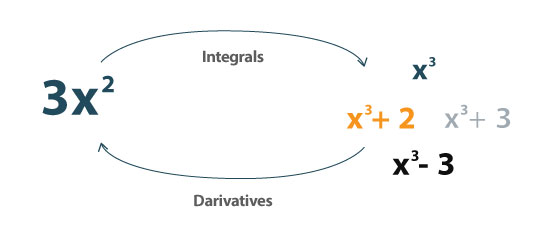
Può essere definito come:
"Un integrale assegna numeri per funzioni in un modo che può descrivere lo spostamento, l'area, il volume e altri concetti che sorgono combinando dati infinitesimali. L'integrazione è una delle due principali operazioni di calcolo; La sua operazione inversa è la differenziazione (prendendo derivati). "
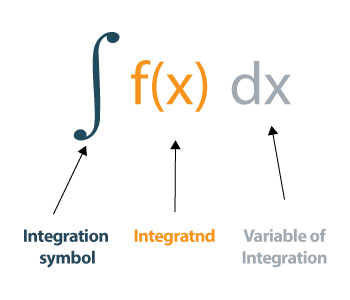
Come valutare gli integrali?
Potresti voler sapere come risolvere manualmente gli integrali. Può essere in qualche modo fastidioso per quelli che stanno appena iniziando con gli integrali. Ma, non preoccuparti. Dimostreremo i calcoli con esempi in modo da poterlo cogliere facilmente.
Usiamo un esempio per capire il metodo per calcolare l'integrale definito.
Esempio - Integrale definito
Per la funzione f (x) = x-1, trova l'integrale definito se l'intervallo è [1, 10].
Soluzione:
Passaggio 1: determinare e annotare la funzione f (x).
F (x) = x – 1
Interval = [1, 10]
Passaggio 2: prendere l'antiderivativo della funzione e aggiungere la costante.
= ∫ (x−1) dx = (x2/2) – x + C
Passaggio 3: calcolare i valori del limite superiore F (A) e il limite inferiore F (B).
AS, A = 1, e B = 10,
F(a) = F(1) = (12/2) - 1 = -0.5
F(b) = F(10) = (102/2) - 10 = 40
Passaggio 4: calcolare la differenza del limite superiore f (A) e il limite inferiore F (B).
F (b) – F (a) = 40 – (-0.5) = 40.5
È possibile utilizzare una doppia calcolatrice integrale sopra se non si desidera indulgere in calcoli integrali.
Esempio: integrale di una funzione trigonometrica
Per la funzione f (x) = sin (x), trova l'integrale definito se l'intervallo è [0, 2π].
Soluzione:
Passaggio 1: scrivi la funzione.
F (x) = sin (x)
Interval = [0, 2π]
Passaggio 2: prendere l'antiderivativo della funzione e aggiungere costante C.
= ∫ sin(x)dx = - cos(x) + C
Passaggio 3: calcolare i valori del limite superiore F (A) e il limite inferiore F (B).
AS, A = 0 e B = 2π,
F (a) = F (0) = cos (0) = 0
F (b) = F (2π) = cos (2π) = 0
Passaggio 4: calcolare la differenza del limite superiore f (A) e il limite inferiore F (B).
F (b) – F (a) = 0 – 0 = 0
Utilizzare il risolutore integrale sopra per risolvere un integrale trigonometrico in una frazione di secondi.