積分 計算機

積分 計算機 は、関数の逆立ちを計算するオンラインツールです。それは定義積分計算機と不定積分計算機として機能し、そしてあなたはすぐに積分値を解くことを可能にします。

積分 計算機積分を評価するために必要なすべての手順を表示します。それは部品ごとに関数を統合し、積分を2つの異なる方法で解決します。

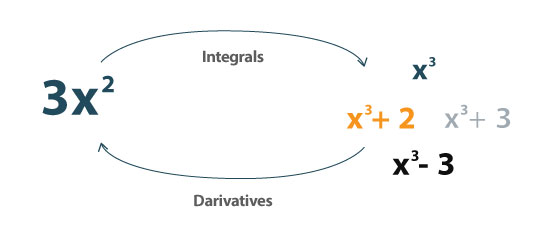
一体のものは何ですか？

積分は派生物の逆です。曲線の下の面積を決定するために使用できます。

それは次のように定義できます。

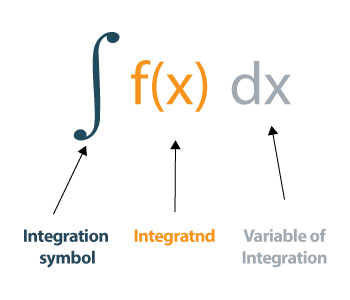
「整数は、微小データを組み合わせることによって発生する変位、面積、ボリューム、およびその他の概念を表すことができる方法で関数に数を割り当てます。統合は計算の2つの主な操作の1つです。その逆動作は区別（採取した派生）です。」

積分を評価する方法

手動で積分を解決する方法を知りたい場合があります。それは積極的なもので始まるものをどういうわけか迷惑になることがあります。しかし、心配しないでください。簡単に把握できるように、例を用いて計算を説明します。

例を使用して、明確な積分を計算する方法を理解しましょう。

例 - 明確な積分
関数f（x）= x - 1の場合、間隔が[1,10]の場合、明確な積分を見つけます。

解決：

ステップ1：関数f（x）を決定して書き込む。

F (x) = x – 1

Interval = [1, 10]

ステップ2：関数の逆立ちを取り、定数を追加します。

= ∫ (x−1) dx = (x²/2) – x + C

ステップ3：上限f（a）および下限f（b）の値を計算する。

A = 1、B = 10

F(a) = F(1) = (1²/2) - 1 = -0.5

F(b) = F(10) = (10²/2) - 10 = 40

ステップ4：上限f（a）および下限f（b）の差を計算する。

F (b) – F (a) = 40 – (-0.5) = 40.5

積分計算に留めておくとしたくない場合は、上記の二重積分計算機を使用できます。

例 - 三角関数の積分
関数f（x）= sin（x）の場合、間隔が[0,2π]の場合、明確な積分を見つけます。

解決：

ステップ1：関数を書き留めます。

F (x) = sin (x)

間隔 = [0, 2π]

ステップ2：関数の逆力を取り、定数Cを加える

= ∫ sin(x)dx = - cos(x) + C

ステップ3：上限f（a）および下限f（b）の値を計算する。

A = 0、B =2π、

F (a) = F (0) = cos (0) = 0

F (b) = F (2π) = cos (2π) = 0

ステップ4：上限f（a）および下限f（b）の差を計算する。

F (b) – F (a) = 0 – 0 = 0

1分の数分で三角関数積分を解くために上記の積分ソルバーを使用してください。