To calculate result you have to disable your ad blocker first.
比例計算
を入力 3 入力値、 4番目 入力は不明である必要があります( バツ )、および計算ボタンを押して、これを使用して2つの画分間の割合を見つけます 比例計算機 次に、
Table of Contents:
割合計算機
この比率計算ツールを使用して、未知の変数の値を解きます。これは、あまり労力をかけずに比率を解くのに役立つオンライン ツールです。このプロポーション ソルバーを使用すると、プロポーションを解決するプロセスが非常に楽になります。
値と変数を入力するだけです バツ 指定されたボックスに入力して X の値を取得します。
割合は何ですか?
あ 割合 は 2 つの量の間の関係を表します。等号で結合された 2 つの分数の 2 つの比率で構成されます。 “=”。 比率は次のように記述できます。
2 : 5 = 7 : 4 または
2/5 = 7/4
“ 数学では、2 つの異なる量が定数に乗算的に関連付けられている場合、それらの量は比例関係にあると言われます。つまり、比率または積のいずれかが定数となる場合です。この定数の値は、比例係数または比例定数と呼ばれます。 ”
比率には主に3種類あります。
正比例:
1 つの変数の量が増加すると、別の変数の量も増加し、その逆も同様です。それは正比例として知られています。
反比例:
1 つの変数の量が増加すると、別の変数の量は減少し、その逆も同様です。それは反比例として知られています。
化合物の割合:
これは、一度に 2 つ以上の数量を処理する比例の一種です。つまり、 2 : 3 : 4 = 3 : 7 : 1
比例を解くにはどうすればよいでしょうか?
学生は試験や教室で割合を手で解かなければなりません。このツールは、課題や宿題をすばやく完了するのに非常に役立ちます。さらに、比例計算の学習にも使えます。ここでは、自分で比率を計算する方法を説明します。
交差乗算法
割合の欠損値または未知の変数を計算するには、次の手順に従います。
- 指定された値を分数形式で書き込みます。未知の値を表すには任意の変数を使用します。
- 等号を使用して両方の分数を結合します。
- 両方の分数を対角的に掛けます。つまり、最初の分数の分子と 2 番目の分数の分母を掛け、2 番目の分数の分子と最初の分数の分母を掛けます。
- 掛け算の後に両方の数値を書き、それらの間に等号を入れます。
- 方程式のどちらかの辺を分離して変数の値を見つけます。
例 –正比例
ソウルから釜山までの列車は300kmの距離を4時間で移動します。 500kmの距離に到達するのにどれくらい時間がかかりますか?
解決 :
ステップ1 : 指定された値を分数形式で書き込みます。未知の値を表すには任意の変数を使用します。
300 km を 4 時間で移動すると、比率は 300 / 4 になります。
500 km の距離の比率は次のようになります: 500 / バツ
ステップ2 : 等号を使用して両方の分数を結合します。
300 / 4 = 500 / バツ
または
300 : 4 = 500 : バツ
ステップ3 その上 両方の分数を対角的に掛けます。つまり、最初の分数の分子と 2 番目の分数の分母を掛け、2 番目の分数の分子と最初の分数の分母を掛けます。
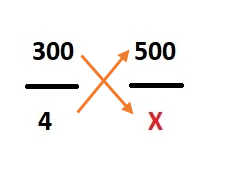
ステップ4 : 掛け算の後に両方の数値を書き、それらの間に等号を入れます。
300 X = 500 × 4
ステップ5: 方程式のどちらかの辺を分離して変数の値を見つけます。
X = 2000 / 300
X = 6.6 約時間
つまり、列車で500kmの距離を移動するには約6時間半かかります。
例 –反比例
おもちゃ製造工場では、3 人の労働者が 8 日間でおもちゃの箱を作ります。同社はユニットの生産量を増やすためにさらに 2 人の労働者を雇用した。現在、工場には合計5人の労働者がいます。同じタスクを 5 人の作業者が完了するのにどれくらい時間がかかりますか?
解決 :
ステップ1 : 指定された値を分数形式で書き込みます。未知の値を表すには任意の変数を使用します。
前後の従業員の比率 = 3 / 5
完了日数の割合 = バツ / 8
ステップ2 : 等号を使用して両方の分数を結合します。
3 / 5 = バツ / 8
ステップ3 : 両方の分数を対角的に掛けます。つまり、最初の分数の分子と 2 番目の分数の分母を掛け、2 番目の分数の分子と最初の分数の分母を掛けます。
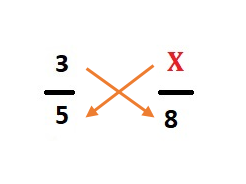
ステップ4 : 掛け算の後に両方の数値を書き、それらの間に等号を入れます。
5 X = 3 × 8
ステップ5 : 方程式のどちらかの辺を分離して変数の値を見つけます。
X = 24 / 5
X = 4.8
したがって、5 人の作業員が約 1 時間でおもちゃを製造します。 4.8 日々。
よくある質問
割合はどのように計算しますか?
比率は交差乗算法を使用して計算できます。交差乗算法では、両方の分数の分子と分母を対角的に乗算し、方程式の片側に分離して未知の変数の値を計算します。
たとえば、次のような 2 つの分数があります。
2/3 = 4/ バツ
交差乗算により、次が得られます。
2 バツ = 12ε; バツ = 6
比率の例は何ですか?
比率の例をいくつか次に示します。
- 私たちは特定の量の食品を調理するために材料の割合を使用します。
- 比率を使用してさまざまなショッピング センターの価格を比較します。
- 建築業者は砂とセメントを砂利に混ぜて、特定の割合で溶液を作ります。
- 化学者は、さまざまな化学物質や薬品の割合を使用して、いくつかの化学式や薬品を作ります。
- 特定の重さと長さのロープ。ロープの長さと重さは比例します。
- あらゆるオブジェクトの形状のサイズは互いに比例する可能性があります。
4対3の比率は何ですか?
4対3の比率は次のように書くことができます。 4:3。 これは、2 番目の数量が最初の数量の 1/3 であることを意味します。
いくつかの当量比 4:3 は:
| 4:3 | 8:6 | 12:9 | 16:12 | 20:15 |
| 24:18 | 28:21 | 32:24 | 36:27 | 40:30 |
| 44:33 | 48:36 | 52:39 | 56:42 | 60:45 |
| 64:48 | 68:51 | 72:54 | 76:57 | 80:60 |
| 84:63 | 88:66 | 92:69 | 96:72 | 100:75 |
1対5の比率は何ですか?
1 対 5 の比率は次のように書くことができます。 1:5。 2 位の数量は 1 位の数量の 5 倍であることがわかります。いくつかの当量比 1:5 は:
| 1:5 | 2:10 | 3:15 | 4:20 | 5:25 |
| 6:30 | 7:35 | 8:40 | 9:45 | 10:50 |
| 11:55 | 12:60 | 13:65 | 14:70 | 15:75 |
| 16:80 | 17:85 | 18:90 | 19:95 | 20:100 |
| 21:105 | 22:110 | 23:115 | 24:120 | 25:125 |