To calculate result you have to disable your ad blocker first.
kalkulator całek
Wprowadź limit funkcji, zmiennej, górnej i dolnej granicy. Wybierz opcję określonej lub nieokreślonej. Naciśnij przycisk Oblicz, aby ocenić integralny krok po kroku za pomocą kalkulatora antrenivative.
Table of Contents:
Integral Calculator to narzędzie online, które oblicza antrenivative funkcji. Działa jako określony kalkulator zintegrowany, a także nieokreślony kalkulator zintegrowany i pozwala rozwiązać wartość integralną w krótkim czasie.
Kalkulator integracji linii pokazuje wszystkie czynności wymagane do oceny całek. Wykonuje integrację funkcji przez części i rozwiązuje integrały z dwiema różnymi metodami.
Co to jest integralna?
Integralną jest odwrotność pochodnej. Może być używany do określenia obszaru pod krzywą.
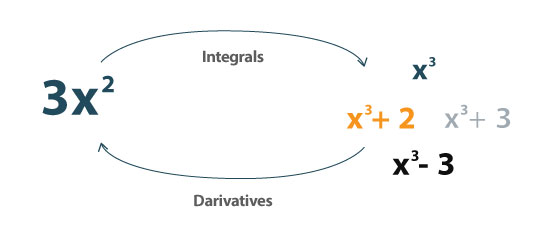
Można go zdefiniować jako:
"Integral przypisuje numery do funkcji w sposób, który może opisać przemieszczenie, obszar, objętość i inne koncepcje, które powstają, łącząc nieskończenie danych. Integracja jest jedną z dwóch głównych operacji rachunków; jego odwrotna operacja jest zróżnicowana (przyjmowanie pochodnych). "
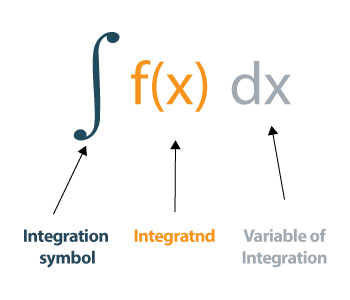
Jak oceniać integrale?
Możesz wiedzieć, jak ręcznie rozwiązać integrały. Może być jakoś irytujący dla tych, którzy dopiero zaczynają się od całek. Ale nie martw się. Zapazujemy obliczenia z przykładami, abyś mógł go łatwo zrozumieć.
Wykorzystajmy przykład, aby zrozumieć metodę obliczenia określonej integralnej.
Przykład - określona integralna
Dla funkcji F (x) = x - 1 znajdź określoną integralną, jeśli przedział wynosi [1, 10].
Rozwiązanie:
Krok 1: Określ i zapisuj funkcję F (x).
F (x) = x – 1
Interval = [1, 10]
Krok 2: Weź antrenivative funkcji i dodaj stałą.
= ∫ (x−1) dx = (x2/2) – x + C
Krok 3: Oblicz wartości górnej granicy f (a) i dolnej limitu F (b).
As, a = 1, and b = 10,
F(a) = F(1) = (12/2) - 1 = -0.5
F(b) = F(10) = (102/2) - 10 = 40
Krok 4: Oblicz różnicę górnej granicy f (a) i dolnej limitu F (b).
F (b) – F (a) = 40 – (-0.5) = 40.5
Możesz użyć podwójnego kalkulatora zintegrowanego powyżej, jeśli nie chcesz się oddawać integralnych obliczeń.
Przykład - integralna funkcji trygonometrycznej
Dla funkcji F (x) = grzech (X), znajdź określony integralny, jeśli przedział wynosi [0, 2π].
Rozwiązanie:
Krok 1: Zapisz funkcję.
F (x) = sin (x)
Interval = [0, 2π]
Krok 2: Weź antrenivative funkcji i dodaj stałą C.
= ∫ sin(x)dx = - cos(x) + C
Krok 3: Oblicz wartości górnej granicy f (a) i dolnej limitu F (b).
As, a = 0, and b = 2π,
F (a) = F (0) = cos (0) = 0
F (b) = F (2π) = cos (2π) = 0
Krok 4: Oblicz różnicę górnej granicy f (a) i dolnej limitu F (b).
F (b) – F (a) = 0 – 0 = 0
Używaj zintegrowanego solvera powyżej, aby rozwiązać integralny trygonometryczny w ułamku sekund.