To calculate result you have to disable your ad blocker first.
интеграл онлайн
Воспользуйтесь нашим калькулятор интегралов (первообразной), чтобы вычислить шаг за шагом интеграл.
Table of Contents:
интеграл онлайн
Интегральный калькулятор — это онлайн-инструмент, который вычисляет первообразную функции. Он работает как калькулятор определенного интеграла, а также калькулятор неопределённого интеграла и позволяет быстро найти целое значение.
Интегральный решатель показывает все шаги, необходимые для вычисления интегралов. Он выполняет интегрирование функции по частям и решает интегралы двумя разными методами.
Что такое интеграл?
Интеграл – это обратная сторона производная. Его можно использовать для определения площади под кривой.
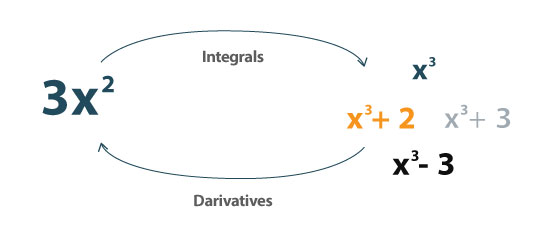
Его можно определить как:
“интеграл присваивает числа функциям таким образом, чтобы можно было описать перемещение, площадь, объем и другие понятия, возникающие при объединении бесконечно малых данных. Интегрирование - одна из двух основных операций исчисления; его обратная операция — дифференцирование (взятие производных). ”
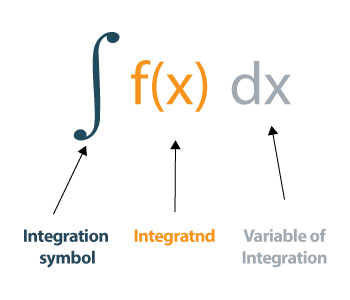
Как вычислить интеграл?
Возможно, вам захочется узнать, как решать интегралы вручную. Это может немного раздражать тех, кто только начинает изучать интегралы. Но не волнуйтесь. Мы продемонстрируем расчеты на примерах, чтобы вы могли легко их понять.
Давайте воспользуемся примером, чтобы понять метод вычисления определенного интеграла.
Пример – Определенный интеграл
Для функции f (x) = x – 1, найдите определенный интеграл, если интервал равен [1, 10].
Решение:
Шаг 1: Определите и запишите функцию Ф(х).
F (х) = х – 1
Интервал = [1, 10]
Шаг 2: Оцените интеграл функции и добавьте константу.
= ∫ (x&минус;1) dx = (x 2 /2) – х + С
Шаг 3: Рассчитать значения верхнего предела Ф(а) и нижний предел Ф(б).
Поскольку a = 1 и b = 10,
F(a) = F(1) = (1 2 /2) - 1 = -0,5
F(b) = F(10) = (10 2 /2) - 10 = 40
Шаг 4: Рассчитать разницу верхнего предела Ф(а) и нижний предел Ф(б).
Ф (б) – F(а) = 40 – (-0,5) = 40,5
Вы можете использовать интегральный калькулятор выше, если вы не хотите заниматься интегральными вычислениями.
Пример – Интеграл тригонометрической функции
Для функции f(x) = sin(x) , найдите определенный интеграл, если интервал равен [0, 2π].
Решение:
Шаг 1: Запишите функцию.
F(x) = грех(x)
Интервал = [0, 2π]
Шаг 2: Оцените интеграл функции и добавьте константу С .
= ∫ sin(x)dx = - cos(x) + C
Шаг 3: Рассчитать значения верхнего предела Ф(а) и нижний предел Ф(б).
Поскольку a = 0 и b = 2π,
F (a) = f (0) = -cos (0) = -1
F (b) = f (2π) = -cos (2π) = -1
Шаг 4: Рассчитать разницу верхнего предела Ф(а) и нижний предел Ф(б).
Ф (б) – F (а) = -1 - (-1) = -1 + 1 = 0
Используйте интегральный решатель, описанный выше, чтобы решить тригонометрический интеграл за доли секунд.
Примеры интегральных
Вот еще несколько примеров межгал, решенных нашим интегральным искателем.
| Функции | Интеграция |
| интеграл от 1/x | log x + C |
| интеграл от 2^x | 2x/ln2 + c |
| Интеграл 2x | x2 + C |
| интеграл от х | x2/2 + C |
| интеграл от e^x | e^x + C |
| интеграл от 1/e^x | -e-x + C |
| интеграл от 1 | x + C |
| интеграл от x^x | Неинтегрируемая функция |
| интеграл от a^x | ax/ln(a) + C |
| интеграл 1/x^2 | -1/x + C |
| интеграл от ln(x) | xlnx - x + C |
| интеграл Sec^2x | tan(x) + C |