Integral hesaplama

Integral hesaplama

Integral hesaplama, bir fonksiyonun ters türevini hesaplayan çevrimiçi bir araçtır. Belirli bir integral hesaplayıcısının yanı sıra belirsiz bir integral hesaplayıcı olarak da çalışır ve integral değerini anında çözmenizi sağlar.

Çizgi entegrasyon hesaplayıcısı, integralleri değerlendirmek için gereken tüm adımları gösterir. Bir fonksiyonun integralini parçalar halinde gerçekleştirir ve integralleri iki farklı yöntemle çözer.

integral nedir?

İntegral, türevin tersidir. Eğrinin altındaki alanı belirlemek için kullanılabilir.

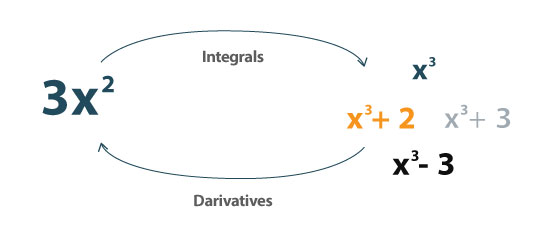
Şu şekilde tanımlanabilir:

"Bir integral, sonsuz küçük verileri birleştirerek ortaya çıkan yer değiştirme, alan, hacim ve diğer kavramları tanımlayabilecek şekilde işlevlere sayılar atar. Entegrasyon, hesabın iki ana işleminden biridir; ters işlemi türev almadır (türev alma).

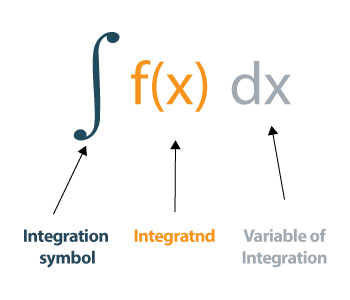
İntegral nasıl değerlendirilir?

İntegralleri manuel olarak nasıl çözeceğinizi bilmek isteyebilirsiniz. İntegrallere yeni başlayanlar için bir şekilde can sıkıcı olabilir. Ama endişelenme. Kolayca kavrayabilmeniz için hesaplamaları örneklerle göstereceğiz.

Belirli integrali hesaplama yöntemini anlamak için bir örnek kullanalım.

Örnek – Belirli integral

f (x) = x – 1 işlevi için, aralık [1, 10] ise belirli integrali bulun.

Çözüm:

1. Adım: F (x) işlevini belirleyin ve not edin.

F(x) = x – 1

Aralık = [1, 10]

2. Adım: Fonksiyonun ters türevini alın ve sabiti ekleyin.

= ∫ (x−1) dx = (x²/2) – x + C

3. Adım: Üst sınır F (a) ve alt sınır F (b) değerlerini hesaplayın.

a = 1 ve b = 10 olarak,

F(a) = F(1) = (1²/2) - 1 = -0.5

F(b) = F(10) = (10²/2) - 10 = 40

4. Adım: Üst sınır F (a) ve alt sınır F (b) arasındaki farkı hesaplayın.

F (b) – F (a) = 40 – (-0.5) = 40.5

İntegral hesaplamalarıyla uğraşmak istemiyorsanız, yukarıdaki çift integral hesaplama yı kullanabilirsiniz.

Örnek – Bir trigonometrik fonksiyonun integrali

f (x) = sin (x) işlevi için, aralık [0, 2π] ise belirli integrali bulun.

Çözüm:

1. Adım: İşlevi yazın.

F (x) = günah (x)

Aralık = [0, 2π]

2. Adım: Fonksiyonun ters türevini alın ve C sabitini ekleyin.

= ∫ sin(x)dx = - cos(x) + C

3. Adım: Üst sınır F (a) ve alt sınır F (b) değerlerini hesaplayın.

As, a = 0, and b = 2π,

F (a) = F (0) = cos (0) = 0

F (b) = F (2π) = cos (2π) = 0

4. Adım: Üst sınır F (a) ve alt sınır F (b) arasındaki farkı hesaplayın.

F (b) – F (a) = 0 – 0 = 0

Bir trigonometrik integral saniyeler içinde çözmek için yukarıdaki integral çözücü kullanın.