To calculate result you have to disable your ad blocker first.
带步骤的积分计算器
输入函数、变量、上限和下限。选择确定或不确定选项。打 计算 按钮使用积分计算器逐步评估积分。
积分计算器
积分计算器是一种计算函数反导数的在线工具。它既可以用作定积分计算器,也可以用作不定积分计算器,让您立即求解积分值。
积分求解器向您显示评估积分所需的所有步骤。它对函数进行分部积分,并用两种不同的方法求解积分。
什么是积分?
积分是积分的逆过程 衍生物。 它可用于确定曲线下的面积。
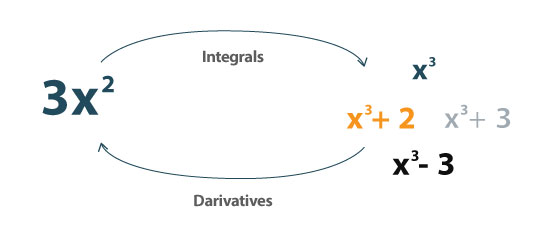
它可以定义为:
“ 一个 积分 以可以描述位移、面积、体积以及通过组合无穷小数据产生的其他概念的方式为函数分配数字。积分是微积分的两个主要运算之一;它的逆运算是微分(求导)。 ”
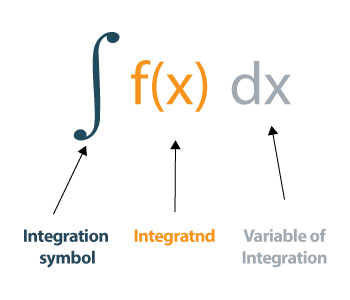
如何评估积分?
您可能想知道如何手动求解积分。对于那些刚刚开始使用积分的人来说,这可能会有点烦人。但是,不用担心。我们将通过示例演示计算,以便您轻松掌握。
我们通过一个例子来了解一下定积分的计算方法。
示例 –定积分
对于函数 f(x)=x—— 1、 如果区间为,求定积分 [1, 10]。
解决方案:
步骤1: 确定并写出函数 F(x)。
F(x)=x—— 1
间隔 = [1, 10]
第2步: 计算函数的积分并添加常数。
= ∫ (x+1) dx = (x 2 /2) – x+C
步骤3: 计算上限的值 F A) 和下限 f(b)。
as,a = 1,b = 10,
f(a)= f(1)=(1 2 /2) - 1 = -0.5
f(b)= f(10)=(10 2 /2) - 10 = 40
步骤4: 计算上限的差 F A) 和下限 f(b)。
f(b) - f(a)= 40 - (-0.5)= 40.5
您可以使用 积分计算器 如果您不想沉迷于积分计算,则上述。
示例 - 三角函数的积分
对于功能f(x)= sin(x) , 如果间隔为 [0, 2π]。
解决方案:
步骤1: 写出该函数。
F(x)=sin(x)
间隔 = [0, 2π]
第2步: 计算函数的积分并添加常数 C 。
= ∫ sin(x)dx = - cos(x) + C
步骤3: 计算上限值 F A) 及下限 F(b)。
由于,a = 0,b = 2π,
F(a) = F(0) = -cos(0) = -1
F(b) = F(2π) = -cos(2π) = -1
步骤4: 计算上限之差 F A) 及下限 F(b)。
F(b)—— F (a) =-1 - (-1) = -1 + 1 = 0
使用上面的积分求解器可以在几分之一秒内求解三角积分。
积分的例子
以下是我们的积分查找器求解的更多积分示例。
| 功能 | 集成 |
| 1/x 的积分 | 对数 x + C |
| 2^x 的积分 | 2x/ln2 + c |
| 2倍的积分 | X 2 + c |
| x的积分 | X 2 /2+C |
| e^x 的积分 | e^x + C |
| 1/e^x 的积分 | -e -X + C |
| 1 的积分 | x+C |
| x^x 的积分 | 非整合功能 |
| A^X的积分 | A X /ln(a) + C |
| 1/x^2 的积分 | -1/x + c |
| LN的积分(x) | XLNX -X + C |
| Sec^2x的积分 | 棕褐色(x) + c |