Binary To Hex Converter

Binary to Hex Converter

Binary to Hex converter is an online tool that helps convert binary numbers into hexadecimal numbers. It makes long calculations simple and easy by just entering the values in the respective fields.

What is the Binary number system?

A binary number system has a base “2” and contains only two elements such as “0 & 1”. It plays a more important role in computer programming to tell whether the statement is true or false.

If any statement is true then it is represented by the digit “1” while on the other hand if a statement is wrong then it is represented by the digit “0”. Its mathematical representation for any number “(b)2”.

Where,

• “b” represents any binary number like (11001, 1010.11, 1110011, etc.).

What is the Hexadecimal number system?

A hexadecimal number system works under the base of 16 and contains the 16 total number of elements. In this system first 10 elements are “0 to 9” and the remaining six elements are represented by the first six English alphabets such as “A, B, C, D, E, and F”.

Its mathematical representation for any number “(a)16”.

Where,

• “a” represents any hexadecimal number such as (197F, 45ED).

Steps to convert the Binary into Hexadecimal number

To convert the binary number into a hexadecimal number first convert the binary to decimal number and then the decimal number is converted into the Hexadecimal number.

For the conversion of binary into the hexadecimal number follow the below steps.

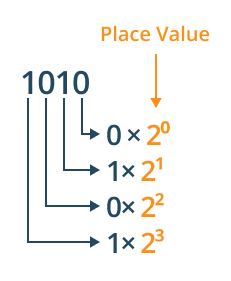
• First, count the total number of digits in the given binary to move from right to left. Then place the value of every digit in the exponent of 2 (exponent starts from zero) for a non-decimal number.

• For decimal numbers, we move in two ways before the decimal point moves from right to left following the above step and after the decimal point, power starts from “-1” to move from left to right.

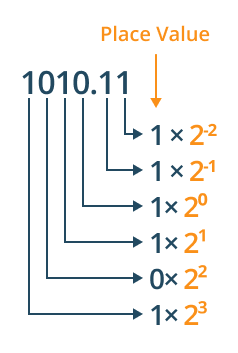
• Write each binary digit with its corresponding power of 2 to move from right to left.
• Solve all powers and add the products.
• Then, the final answer is the required decimal number.
• Lastly, the decimal number is converted into the hexadecimal number by factorization with the number “16”.

Example 1:

Convert the given Binary number “110011” into the Hex-number.

Solution:

Step 1: Firstly, convert the given binary number into a decimal number.

For this conversion place the position value in the exponent of the “2” with the multiple of its placement number.

(110011)₂ = (1 × 2⁵) + (1 × 2⁴) + (0 × 2³) + (0 × 2²) + (1 × 2¹) + (1 × 2⁰)

     = (1 × 32) + (1 × 16) + (0 × 8) + (0 × 4) + (1 × 2) + (1 × 1)

By simply and adding all values get the required number.

     = (32) + (16) + (0) + (0) + (2) + (1)
     = 51

Step 2: For the conversion of the above decimal into Hex factorize them by “16”.

Thus, get the binary to hex-number. 

(110011)2 = (33)16

Example 2:

Convert the given Binary number “1111.0011” into the Hex-number.

Solution:

Step 1: Firstly, convert the given binary number into a decimal number.

For this conversion place the position value in the exponent of the “2” with the multiple of its placement number.

(1111.0011)₂ = (1 × 2³) + (1 × 2²) + (1 × 2¹) + (1 × 2⁰) + (0 × 2⁻¹) + (0 × 2⁻²) + (1 × 2⁻³) + (1 × 2⁻⁴)

          = (1 × 8) + (1 × 4) + (1 × 2) + (1 × 1) + (0 × 1/2) + (0 × 1/4) + (1 × 1/8) + (1 × 1/16)

By simply and adding all values get the required number.

           = (8) + (4) + (2) + (1) + (0) + (0) + (1/8) + (1/16)

           = (8) + (4) + (2) + (1) + (0.125) + (0.0625)

(1111.0011)₂ = (15.1875)₁₀

Step 2: For the conversion of the above decimal into Hex factorize them by “16”.

To find the Hex-number of decimal numbers we distribute our number into two parts before and after the decimal point.

Before decimal point number = 15

After decimal point number = 1875

We know “15” represent the Alphabet “F”

Thus, write the answer before decimal point number before the decimal point, and after the decimal point number after the decimal point.

(110011)2 = (F.3)16